Existe un refrán galés originado en 1860 que dice: “Eat an apple on going to bed, and you’ll keep the doctor from earning his bread”. Esta frase ha sufrido modificaciones a lo largo del tiempo y es así como hoy en día se ha transformado en “An apple a day keeps the doctor away“. Si deseáramos adaptar todavía más esta frase al ámbito médico, podríamos simplemente cambiar la palabra «apple» por «aspirina»
De esta manera queda conformada una hipótesis; «Una aspirina al día mantiene al doctor en la lejanía». Pero… ¿Cómo podemos saber si esto realmente es así?, ¿Cómo sabemos si la hipótesis planteada es verdadera?, ¿De qué depende que una hipótesis se torne falsa?
La hipótesis y su problemática
Una hipótesis es algo que se supone como cierto o verdadero. Desde el punto de vista del Método Científico es una solución provisoria que aun no ha sido comprobada y que puede presentar distintos grados de fiabilidad. Una vez que esta queda verificada, pasa a ser un enunciado.
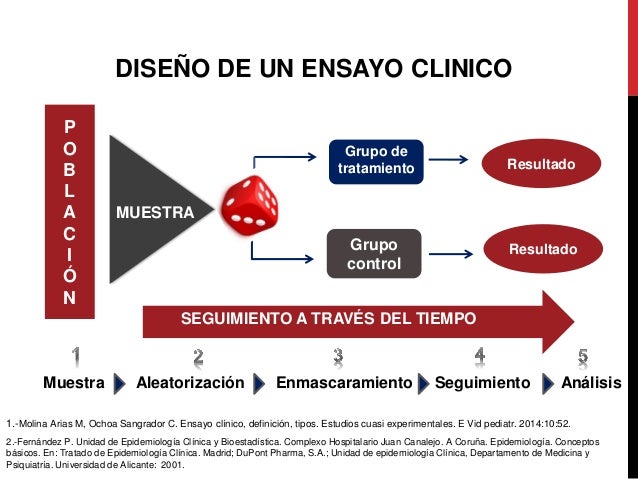
Las investigaciones que se realizan en el terreno de la medicina suelen ser del tipo comparativas. Es decir, se toman muestras poblacionales aleatorias y se analiza el efecto que producen los tratamientos en ellas. Su finalidad es observar qué tan efectivo es determinado fármaco o cómo responden los individuos a determinada terapia.
El problema que se nos plantea es si los resultados que obtenemos durante la investigación están dados por los efectos propios del fármaco o por alguna característica especial que pudieran llegar a tener los individuos de nuestra muestra tomada al azar.
Aquí es cuando entran en escena los Test de Contraste de Hipótesis y los errores asociados a ellos.
Test de Contraste de Hipótesis
También denominado prueba de significación; es un procedimiento basado en la evidencia de una muestra y en la teoría de probabilidades, usado para determinar si la hipótesis es una afirmación razonable.
En este test debemos enfrentar dos hipótesis opuestas formuladas al inicio del estudio. Una de ellas, la “suposición a favor”, es la hipótesis nula (H0). La hipótesis alternativa (H1) será la que se acepte cuando la hipótesis nula sea rechazada.
Si aplicamos esto a nuestro ejemplo, podemos establecer que:
- H0: «Una aspirina al día mantiene al doctor en la lejanía»
- H1: «Una aspirina al día NO mantiene al doctor en la lejanía» (o alguna hipótesis similar)
Durante la investigación siempre se empieza suponiendo que la H0 es verdadera. Se utilizarán los datos de la muestra para decidir si la evidencia está mas a favor de H0 o de H1. A partir de esto se obtiene una conclusión:
- Se acepta H0 y queda como verdadera
- Se rechaza H0 y queda como verdadera H1
La hipótesis nula se rechaza solo si los datos ofrecen suficiente evidencia para no considerarla verdadera
Pero aquí, volvemos a una de nuestras incógnitas iniciales.
El problema que se nos plantea es si los resultados que obtenemos durante la investigación están dados por los efectos propios del fármaco o por alguna característica especial que pudieran llegar a tener los individuos de nuestra muestra tomada al azar.
Se han realizado innumerables estudios sobre el efecto de la aspirina en los adultos mayores. Algunos llegan a la conclusión que la aspirina tiene un efecto favorable mientras que otros no solo no han visto ninguna mejoría en la salud, sino que ademas, aumenta el riesgo de hemorragias considerables (3).
Supongamos que se dispone de una población de 1.000 individuos y que para el estudio usaremos 5 muestras de 200 personas seleccionadas al azar. Los resultados no serán los mismos en todas las muestras al finalizar el estudio. Las diferencias se le van a atribuir al azar y no específicamente al fármaco que estemos probando, en este caso, la aspirina.
Entonces, ¿Cómo determinamos cuanta es suficiente evidencia?
Aquí entra en juego lo que se conoce como Nivel de Significancia, que es la probabilidad de rechazar la H0 cuando realmente es verdadera. En otras palabras, nos da un criterio para determinar si se tiene suficiente evidencia para descartar nuestra hipótesis nula. Un nivel de significancia aceptable varía entre 1 y 5%, ya que lo que menos queremos es que nuestra hipótesis nula sea rechazada cuando las probabilidades de ser verdadera son altas.
Al estar estudiando muestras y no una población entera, podemos cometer errores asociados a la aceptación o rechazo de la hipótesis nula. Se los conoce como errores alfa y beta.
- Error alfa o tipo 1: se comete cuando se rechaza una hipótesis que es correcta
- Error beta o tipo 2: se comete cuando se acepta una hipótesis que es incorrecta
Entonces; en el error alfa podemos decir que por causa del azar (patologías o condiciones de cada paciente) la aspirina no tiene ningún beneficio; y por otro lado, en el error beta y también por causa del azar (pacientes sin patologías) se acepta que la aspirina si es beneficiosa. En este ultimo caso, terminaríamos exponiendo a los pacientes a posibles hemorragias de gran calibre.
En definitiva, las pruebas de contraste de hipótesis intentan aceptar o rechazar una hipótesis nula, calculando la probabilidad de que los resultados obtenidos sean producto del azar. Gracias a ellas podemos calcular que tan probable es que en una investigación los resultados estén condicionados y determinados por el azar y que las diferencias que observamos sean debido a eso.
Referencias:
- Pruebas de contraste de hipótesis. Estimación puntual y por intervalos. Ágata Carreño Serra. SEDEN, Sociedad Española de Enfermería Nefrológica.
- Introducción a la probabilidad y estadística. Mendenhall, Beaver, Beaver. Cengage Learning. 2010. ISBN-13: 978-607-481-466-8
- Effect of Aspirin on Disability-free Survival in the Healthy Elderly. John J. McNeil, M.B., B.S., Ph.D., Robyn L. Woods, Ph.D., Mark R. Nelson, M.B., B.S., Ph.D. The New England Journal of Medicine DOI:10.1056/NEJMoa1800722
- Why an aspirin a day no longer keeps the doctor away …Marie Lordkipanidzé. University of Birmingham, Edgbaston, Birmingham, UK. doi: 10.1160/TH10-11-0749