Las “Pruebas paramétricas y no paramétricas “son una parte importante de la bioestadística y constituyen excelentes herramientas a la hora de resumir y presentar datos obtenidos de una investigación. El objetivo principal del artículo es introducir los conceptos básicos considerados necesarios para el buen entendimiento de la utilidad que estas pruebas pueden brindarnos. Como objetivo secundario se pretende que el artículo sirva de guía al lector en la elección de las pruebas adecuada en base a sus propósitos de investigación.

PRUEBAS PARAMÉTRICAS

Para comenzar con el desarrollo del tema se proponen 3 situaciones habituales en la práctica médica.

Situación A: Nos encontramos frente a un paciente adulto de 58 años de edad, consulta porque anteriormente le han medido la tensión arterial en la farmacia y le dijeron que estaba elevada.

Situación B: Un niño de 4 años es traído a consulta pediátrica. El motivo es una evaluación periódica de la salud y su madre quiere saber si el niño crece normalmente.

Situación C: Su amigo le da sus estudios de laboratorio para que los interprete y quiere saber si sus valores de glucemia plasmática en ayunas son normales.

De las tres situaciones podemos observar un patrón que se repite, la necesidad de
darle un contexto práctico y útil a los valores que tenemos al frente. En cualquier situación se evidencia la necesidad de un parámetro. Gran parte de las acciones médicas se encuentran respaldadas en parámetros.
Si en la situación A, medimos la tensión arterial del paciente y encontramos un valor por encima de 130/85 milímetros de mercurio, diremos al menos que no es normal ( SAC, 2018) . Al igual que en la situación B si observamos que el niño solo aumentó su talla respecto al año anterior en 1 centímetro (WHO, 2009) o la situación C que el valor de glucemia plasmática en ayunas resultó ser de 80 mg/dl en su estudio de laboratorio y se encuentra dentro de parámetros normales (SAD, 2016) . Sin la existencia de parámetros todos los datos obtenidos carecerían de sentido y la decisión médica dependería del criterio de cada profesional, situación totalmente contraria a la que se necesita en medicina.

SAC: Sociedad Argentina de Cardiología
WHO: World Health Organization
SAD: Sociedad Argentina de Diabetes

La estadística nos brinda la posibilidad de ordenar la evidencia obtenida, cuantificar sus valores y utilizarlos para mejorar la terapéutica ( Glantz,2003).

Los parámetros se obtienen de estudiar a la población . La evidencia que obtenemos de dichos estudios componen las bases de la medicina actual, conocida como medicina basada en la evidencia (Cobo, 2007)

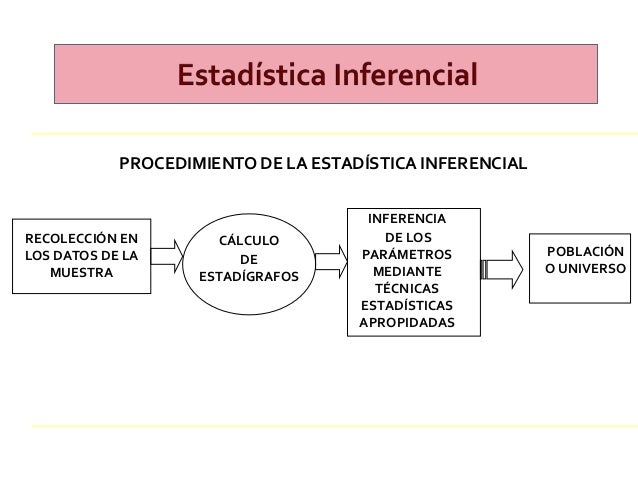
Estadística inferencial

La estadística inferencial responde a dos propósitos vinculados entre sí (Sampieri, 2010)

• Estimar parámetros
• Probar hipótesis

Parámetros poblacionales

Los parámetros son las estadísticas de la población. Los parámetros reales normalmente no son conocidos ya que significaria un enorme costo y muchísimo tiempo estudiar a toda la población. Por este motivo se recurre a tomar muestras de la población que se quiere estudiar. Dichas muestras deben ser tomadas de forma aleatoria, para que todos los habitantes tengan las mismas posibilidades de participar del estudio y de esta manera reducir al mínimo el sesgo de selección. Sus resultados estadísticos son los estadígrafos. Los estadígrafos forman para de las medidas de tendencia central y la más utilizada es la media.
A través de la inferencia estadística podemos utilizar los estadígrafos para estimar parámetros. ( Sampieri, 2010).

Estadística paramétrica

Según Sampieri ( 2010) la estadística paramétrica debe partir de los siguientes supuestos.

• El nivel de medición de las variables está dado por intervalos o razón
• La distribución de la variable dependiente medida es normal.
• Si dos poblaciones o más son estudiadas, su varianza debe ser homogénea, es decir que sus datos deben tener una dispersión similar (Wiersma y Jurs, 2008).

Escalas de medición

Cuando medimos una variable debemos cuantificarla y expresar sus resultados en unidades que contengan un lenguaje común a cualquier observador ( Cobo,2007).
Por este motivo se expresan los datos en escalas. Las escalas pueden ser nominales, ordinales , de intervalo o de razón.

Escala Nominal: Agrupa unidades con similares características permitiendo establecer categorías. Por ejemplo: dos categorías ampliamente conocidas; Agudo o grave. Las patologías agudas comparten características en común que las diferencian de las patologías crónicas.

Escala Ordinal: Como la palabra lo dice, esta escala permite establecer una relación de orden . Por ejemplo: leve, moderado y grave. Otro ejemplo podría ser la cantidad de cruces en base a la concentración proteica de una muestra de orina. +/++/+++.

Escala de intervalo: Un intervalo es una distancia X entre dos valores. Por ejemplo, la distancia medida en años entre 59 y 60 es igual a 1. Si la distancia entre todos los intervalos es igual, se puede hablar de unidad de medida. Entonces el intervalo entre 10 y 11 años es el mismo que entre 30 y 31. Si no disponemos de unidades de medida, entonces los saltos entre intervalos no serán iguales.

Escala de razón: En la escala de razón, el valor cero es absoluto, esto quiere decir que implica la ausencia total del atributo. Por ejemplo, si medimos la variable “Kilogramos”, el valor cero indica su ausencia absoluta.

Distribución normal y desvío estándar

Cuando estudiamos una población determinada, resumimos sus datos con la media, que representa el centro de la distribución, pero creer que la totalidad de los valores rondan en la media implicaría perder toda la valiosa información que la variabilidad nos ofrece.
El desvío estàndar o desviación típica representa el alejamiento prototípico de la media (Cobo, 2007).

Ejemplo práctico Nº1

Los profesores de la materia “ investigación aplicada y formulación de proyectos” desean averiguar cuál fue la media de notas obtenidas por los alumnos en la última evaluación parcial de la materia .
La media calculada luego de procesar los datos corresponde al valor 7( siete).

Cobo (2007) sostiene que utilizar el calculo de la media por si solo resulta insuficiente, pues debemos saber de qué manera varían o se dispersan los valores respecto a la media y en qué intervalos lo hace.

Ejemplo práctico Nº2

El decano de la Universidad Abierta Interamericana pretende averiguar la media de promedios con el que egresan los alumnos de medicina de dicha universidad. Además está interesado en saber en qué rango de notas se encuentra la mayoría y si su distribución es normal.

Se dice que una muestra se distribuye de forma normal cuando sus valores se concentran alrededor de la media (Glantz, 2003). Para representarlo mejor se propone la siguiente imagen.

El desvío estándar o desviación típica como dijimos antes, es la medida del grado de dispersión o alejamiento del centro y se simboliza con la letra griega sigma minúscula (  σ ). El cálculo del desvío estándar se realiza mediante la siguiente fórmula.

Para explicar cómo se realiza el cálculo del desvío estándar utilizaremos el ejemplo de los profesores pero con un N de 10.

Cada valor o nota obtenida se representa con X y un subíndice. Existen tantos X como notas obtenidas, en este caso, 10.

Las notas obtenidas fueron:

7

6

7

8

9

6

6

7

6

8

La suma de todos los valores dividido por N nos da una media de 7.

Para calcular el desvío estándar solo queda reemplazar en la fórmula. Cada X con su respectivo subíndice representa la nota obtenida y X con el guion encima representa la media de la muestra. Reemplazamos los datos, los elevamos al cuadrado y sumamos todos sus resultados. Al resultado lo dividimos por N y obtenemos el desvío estándar ( DE)

Por cuestiones de tipificación pasaremos directo al resultado.

DE=1

Esto quiere decir que cada 1 punto en la escala que me aleje de la media, tanto hacia arriba o hacia abajo constituye un desvío estándar.
La totalidad del área bajo la curva incluye al 97 % de resultados posibles. Esto se da entre -3 y + 3 desvíos estándar. Si miramos en la imagen anterior, el 68% de las notas caerán en el intervalo entre 6 y 8, comprendidos por un desvio hacia arriba y un desvio hacia abajo. Si usamos un intervalo más amplio comprendido entre -2 DE y +2DE encontraremos el 95,5 % de las notas. y si por último utilizamos el intervalo entre -3 y +3 incluiremos el 99,7 % de las notas.

Con estos simples pasos podremos obtener información valiosa acerca de la forma en que se distribuye nuestra muestra.

Si se desea una explicación mas detallada se recomienda consultar el siguiente enlace: Para mayor entendimiento del tema se propone ver el siguiente video: https://www.youtube.com/watch?v=phY8Z9-TXCY&list=PLwCiNw1sXMSBwU_UiiqvIctctvFICYkKC

La máquina de dalton constituye una forma muy didáctica de entender que es una distribución normal. Se recomienda consultar el video a continuación .https://www.youtube.com/results?search_query=maquina+de+dalton

varianza

Segun Cobo (2003)

“La varianza es el promedio de las distancias con la media elevadas al cuadrado. La desviación típica es su raíz cuadrada y valora el promedio de las distancias con la media: representa la distancia típica o esperada de una observación con la media“.

Para la ampliación del tema se recomienda:
https://youtu.be/cg4kUsbjQms?t=49

Prueba de hipótesis

Como dijimos anteriormente se utiliza la inferencia estadística para la puesta a prueba de hipótesis y comenzaremos con un ejemplo.

Ejemplo práctico Nº3

Un investigador quiere saber si la variable violencia familiar en adolescentes está relacionada con mayores índices de depresión, comparado con aquellos adolescentes que viven en un ambiente familiar sin violencia.

Las hipótesis correspondientes serían:

---

H0 o hipótesis nula : “Los adolescentes que sufren violencia familiar no presentan mayores índices de depresión que aquellos que viven en entornos familiares sin violencia”

y la H1 o Hipótesis alternativa:” Los adolescentes que sufren violencia familiar presentan mayores indices de depresión que aquellos que viven en entornos familiares sin violencia”

---

Como dijimos anteriormente, el propósito del investigador muchas veces es realizar un estudio y poder generalizar sus estadísticas a toda la población. En el ejemplo anterior podríamos tomar una muestra representativa y tomar sus datos. La inferencia estadística se encarga de reunir sus datos en forma de estadísticos y estimar los parámetros. (Sampieri, 2010) Resulta necesario entonces introducir los conceptos de ” Distribución de medias muestrales” y ” Nivel de significancia“.

La distribución de medias muestrales es la manera mas cercana de representar los parámetros, que insistimos, no conocemos sus valores reales, solo los inferimos con el menor grado de error posible.

Ejemplo práctico Nº4

Si nuestra población de interés fueran los adultos diabéticos podríamos estudiar cualquier variable en relación a su enfermedad. Por lo que podríamos tomar muestras representativas de dicha población y estudiarlas. Para cada muestra obtendremos una media, y la media de todas las medias representa la distribución de medias muestrales.
Sampieri (2010) dice en su libro “Si calculáramos la media de todas las medias de las muestras, prácticamente obtendríamos el valor de la media poblacional”

Pero ¿ Cómo aseguro que mi media muestral es congruente con la media poblacional y no fue una mera casualidad ? Para poder generalizar con cierto grado de confianza es que el investigador estima a priori el “Nivel de significancia” ( Sampieri,2010 ).

Existen dos niveles de significancia y se estiman en términos de probabilidad.

Nivel 0.05 Donde el investigador tiene 95% de seguridad en afirmar que los valores de su media muestral se acercan a los valores de la distribución de medias muestrales, que recordemos son muy similares a los parámetros y 5% de equivocarse.

Nivel 0.01 Donde las probabilidades se reducen a 99 % y 1 %.

Se intenta estimar los parámetros con la mayor seguridad posible, pero siempre pueden cometerse errores al probar una hipótesis (Sampieri, 2010). Las posibilidades son:

• Tomar decisiones correctas, como aceptar una hipótesis verdadera o rechazar una hipótesis falsa.
• Rechazar una hipótesis verdadera ( error tipo 1 o alfa) y aceptar una hipótesis falsa ( error del tipo 2 o Beta)

---

Finalmente, habiendo explicado todos los conceptos necesarios para comprender el tema, podemos pasar al desarrollo de las pruebas paramétricas disponibles para el contraste de hipótesis.

Según Sampieri (2010), las pruebas paramétricas más utilizadas son:

• Cociente de correlación de pearson
• Prueba t de student
• Prueba de contraste de la diferencia de proporciones
• Análisis de varianza unidireccional (ANOVA=
• Análisis de varianza factorial
• Análisis de Covarianza ( ANCOVA)

Cociente de correlación de Pearson

Prueba paramétrica utilizada para evaluar la relación entre dos variables medidas en escala de intervalo o razon”. Por ejemplo: ” A mayor X, menor Y” ” a Menor X, mayor Y” ” A mayor X mayor Y” etc.

El coeficiente obtenido se simboliza con la letra r y varía de -1.00 a +1.00

Una puntuación de +1.00 implica correlación positiva perfecta. Es decir que por cada unidad que aumenta de la variable A se condice con un incremento en igual cantidad de la variable B. Algo similar ocurre con el valor -1.00 o correlación negativa perfecta. Por ejemplo,” a mayor X menor Y” en proporciones constantes. Los niveles intermedios representan correlaciones más débiles y el cero indica ausencia absoluta de correlación”

(Sampieri, 2010)

Prueba t de Student

Esta prueba estadística se utiliza para evaluar diferencias entre dos grupos. Por ejemplo , se quiere saber si la media de promedios de los alumnos egresados de medicina de la Universidad Abierta Interamericana difiere de la media de los alumnos de la Universidad de Buenos Aires. Se aplican tantas pruebas t como tantas variables se pretendan medir. La prueba t se puede utilizar también en el contexto experimental. Por ejemplo, se aplica una prueba t a dos grupos antes de la intervención y otra luego de la intervención.
(Sampieri, 2010)

Prueba de diferencia de proporciones

Como la palabra lo dice, la prueba evalúa diferencia de proporciones entre dos grupos, se puede medir en escala de intervalo o razón pero los resultados siempre se expresan en porcentajes. (Sampieri,2010)

Ejemplo práctico Nº5

El jefe de terapia intensiva quien saber si el porcentaje de pacientes hospitalizados por covid-19 que necesitan asistencia respiratoria mecánica en Buenos Aires es mayor que en New York.

Análisis de varianza unidireccional

Así como la prueba t compara diferencias entre dos grupos, ANOVA sirve para comparar tres o más grupos. La prueba nos indica cuánto se diferencian la distribución de medias entre los grupos, pero no nos informa a favor de cual. (Sampieri,2010)

PRUEBAS NO PARAMÉTRICAS

Sampieri (2010) asume que el análisis no paramétrico debe partir de los siguientes supuestos:

• No requieren que la población estudiada se distribuya de manera normal, aceptan distribuciones no normales.
• No es condición excluyente que las variables sean medidas en escala de intervalos o razón.

La estadistica no paramétrica presenta algunas desventajas, como ser que sus datos son menos confiables que en la estadística paramétrica y sus datos no informan acerca de la magnitud de la diferencia entre variables medidas. Por lo cual, se desconocen la distribución de los fenómenos estudiados. (Taylor, 2008)

Segun Sampieri(2010) las pruebas no paramétricas más utilizadas son:

• La chi cuadrada o χ².
• Los coeficientes de correlación e independencia para tabulaciones cruzadas.
• Los coeficientes de correlación por rangos ordenados de Spearman y kendall.

Otras pruebas no paramétricas utilizadas frecuentemente son la prueba de los rangos con signo de Wilcoxon (Taylor, 2008) y la prueba de kruskal-wallis (Triola, 2004).

Como no sabemos la distribución del fenómeno intentamos solucionarlo con alguna de estas pruebas, para conocer la naturaleza del mismo, y así luego poder estudiarla en profundidad y establecer sus parámetros. Podría decirse que la estadistica no parametrica es un primer enfoque orientativo para proceder a evaluar con pruebas paramétricas. (Glantz, 2003)

Según Triola (2004) las pruebas no paramétricas presentan algunas ventajas y desventejas.

A continuación se desarrolla Chi cuadrada. La ampliación de las demás pruebas quedarán a cargo del lector.

Chi cuadrada

Chi cuadrada o ji cuadrado es una prueba no paramétrica utilizada para contrastar hipótesis de tipo correlacionales medidas de forma categórica. No evalúa causalidad sino correlación. Básicamente la distribución Chi cuadrada intenta probar la existencia de relación o no entre variables, o mejor dicho, evalúa si funcionan de manera independiente o no. (sampieri, 2010)

Una variable independiente es aquella que no varia en sus valores por la influencia de otra. por ejemplo la edad de una persona. ( Glantz, 2003 )

Ejemplo práctico Nº6

Un profesor desea evaluar si la sensación de malestar universitario ( variable 1) se relaciona con el hecho de adeudar materias de años anteriores. Los datos en este caso toman valores categóricos. SI o NO, Entonces se generan las hipótesis de la siguiente manera:

H0= El hecho de adeudar materias de años anteriores no está relacionado con la sensación de malestar universitario.

y la H1=El hecho de adeudar materias de años anteriores esta relacionado con la sensación de malestar universitario.

Se obtienen los datos, de una encuesta por ejemplo y se los vuelca en una tabla, llamada tabla de contingencia. (Sampieri, 2010)

Sensación de Malestar	Adeuda Materias
	SI	NO
SI	20	25
NO	10	45

Los datos volcados constituyen frecuencias. Para calcular Chi cuadrado: debemos ampliar la tabla.

Sensación de Malestar	Adeuda Materias
	SI	NO
SI	20	25	45
NO	10	45	55
	30	70	100

En la tabla se puede observar como la suma del total de las filas es igual a la suma del total de las columnas. Si extrapolamos los cuatro valores centrales obtenemos una tabla así

Ahora debemos calcular la frecuencia esperada que se obtiene del cociente entre el total de la columna por el total de la fila y el total. Una vez calculada la frecuencia esperada se procede a calcular Chi cuadrado:

Una vez obtenido el Chi calculado se calcula Chi crítico teniendo en cuenta nivel de significancia y los grados de libertad. El valor obtenido de Chi crítico se lo compara con Chi calculado. Si el calculado resulta mayor que el crítico, se acepta la hipótesis alternativa y si resulta menor, se adopta la hipótesis nula (Sampieri, 2010).

Conclusiones

En base al desarrollo del articulo podemos concluir que la elección entre una prueba paramétrica o una prueba no paramétrica debería estar basada centralmente en el conocimiento de la distribución de la población en estudio y el tipo de datos que se quieran obtener. Si nuestra población se distribuye normalmente resulta conveniente utilizar el análisis paramétrico, pero si desconocemos su distribución, un muy buen acercamiento resulta de utillizar estadistica no paramétrica.

Bibliografía

• TAYLOR, B. R. (2008). BIOESTADISTICA. MÉXICO: PEARSON EDUACIÓN.
• CARDIOLOGIA, S. A. (2018). Consenso Argentino de Hipertensión Arterial. REVISTA ARGENTINA DE CARDIOLOGIA , 6.
• Diabetes, S. A. (2016). Guía para el tratamiento de la diabetes mellitus tipo 2. Revista de la sociedad Argentina de Diabetes .
• Erik Cobo, P. M. (2007). Bioestadística para no estadísticos. EL SEVIER MASSON.
• Triola. F. M. (2004). ESTADÍSTICA novena edición. México: PEARSON.
• Glantz, S. A. (2003). Bioestadistica- 6ta edición. México: McGraw Hill.
• Roberto Hernandez Sampieri, C. F. (2010). Metodologìa de la investigación- 5ta edición. México: Mc Graw-Hill.
• Salud, O. M. (2009). Manual WHO Anthro para computadoras personales versión 3. Ginebra.