El presente trabajo tiene como objetivo brindar información acerca del uso de las herramientas estadisticas para realizar una prueba estadistica y aplicarlas de manera correcta en nuestro proyecto de investigación.
Seguí leyendo “¿Cómo elegir una prueba estadística que voy a aplicar? ¿De qué depende?”¿Qué es la distribución muestral? ¿Qué tipos existen muestral?
Objetivo educativo:
El objetivo de este trabajo es adquirir conocimiento acerca de una parte de la bioestadística que es la distribución muestral, que habla de hacer cuentas de probabilidad, a partir de una parte de la población, visando entender que es una población, una muestra, un muestreo y saber la diferencia entre los tipos de distribución y saber cuándo utilizarlas.
Desarrollo del tema:
¿QUE ES UNA DISTRIBUCIÓN MUESTRAL?
Es una parte de la estadística que es necesario su compresión para desenvolver herramientas metodológicas, como para hacer estudios de una determinada muestra, en una determinada población haciendo y trabajando con probabilidades.
Una distribución muestral es una distribución de muestras estadísticas que se obtienen, por lo regular, de una o más poblaciones. (TAYLOR)
Para hacer una distribución muestral, necesito un muestreo que es una técnica de selección a partir de una población de una muestra; que se va considerar todas las muestras posibles para una determinada población. A partir de estas muestras se calcula la probabilidad, y también se puede estimar el error para la muestra. La muestra se toma de manera aleatoria, sea una muestra simple o compleja, para evitar los sesgos que es la diferencia sistemática entre las características de los miembros de la muestra y la población de la que se obtuvo. (GLANTZ, SEXTA EDICIÓN)
La elaboración de una distribución va depender de: una población que va tener datos que van generar un parámetro µ o p, y va depender de una muestra que va generar un estadístico x o p, donde la población es la totalidad de elementos que interesa estudiar, normalmente no es estudiada toda la población; el muestreo que es parte de la población que ha de estudiarse, con el objetivo de tener resultados generalizados a toda la población y una muestra que tiene que ser de características similares de la población completa a fin de que sea representativa.
Cuando hablamos de las distribuciones muestrales vamos a tener dos clasificaciones, donde una variable aleatoria significa que tiene un numero único y es determinado al azar, en cuanto una variable aleatoria discreta tiene un número finito de valores y la continua un número infinito de valores.
- Distribución de Variables Aleatorias Discretas: Binomial, Poisson, Hipergeométrica
- Distribución de Variables Aleatorias Continuas: Normal
- DISTRIBUCIÓN NORMAL
Es utilizado para representar la distribución de variables cuantitativas, o sea, tiene un infinito de valores. Este tipo de distribución tiene la conocida forma de campana o montaña, y para hacer una distribución normal es necesario la determinación de los parámetros:
- Media (µ) que representa el centro de gravedad, es decir, aquel punto que permitirá aguantar en equilibrio, la distribución. (Bioestadística para no estadísticos)
- Desviación típica (σ) es la distancia con la media del punto de máxima pendiente (Bioestadística para no estadísticos).
- Es una distribución simétrica.
- Es asintótica, es decir sus extremos nunca tocan el eje horizontal, cuyos valores tienden a infinito.
- En el centro de la curva se encuentran la media, la mediana y la moda.
- El área total bajo la curva representa el 100% de los casos.
- Los elementos centrales del modelo son la media y la varianza. (Ricardi, 2011)
- Representación gráfica

Se dice que muchos fenómenos en el campo de la salud se distribuyen normalmente. Esto significa que si uno toma al azar un número suficientemente grande de casos y construye un polígono de frecuencias con alguna variable continua, por ejemplo peso, talla, presión arterial o temperatura, se obtendrá una curva de características particulares, llamada distribución normal. Es la base del análisis estadístico, ya que en ella se sustenta casi toda la inferencia estadística. (Ricardi, 2011)
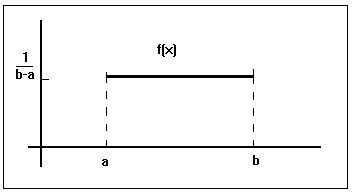
La distribución uniforme, es una parte adentro de la distribución normal, que es una variable aleatoria continua que sus valores se dispersan uniformemente a través del rango de posibilidades. La gráfica de una distribución uniforme presenta una forma rectangular. (TRIOLA, 2005)
2- DISTRIBUCIÓN BINOMIAL
Las distribuciones de probabilidad binomial son importantes porque nos permite enfrentar circunstancias en las que los resultados pertenecen a dos categorías relevantes. (TRIOLA, 2005)
Un experimento binomial presenta las siguientes propiedades:
- Consiste en un número fijo, n, de pruebas idénticas.
- Cada prueba resulta en uno de dos resultados: éxito, S, o fracaso, F
- La probabilidad de éxito en una sola prueba es igual a algún valor p y es el mismo de una prueba a la otra. La probabilidad de fracaso es igual a q=(1-p)
- Las pruebas son independientes (WACKERLY, SÉPTIMA EDICIÓN)
Vale recordar que en una distribución binomial E y F (éxito y fracaso) denotan las dos categorías posibles de todos los resultados, p y q denotan las probabilidades de E y F respectivamente, donde P(E)= p y P(F)= 1-p = q. (TRIOLA, 2005)
Ejemplo de distribución binomial sacado del libro Mario Triola (TRIOLA, 2005)
Un profesor planea aplicar un examen sorpresa de opción múltiple, cada una con 5 respuestas posibles (a,b,c,d,e), pero solamente una es correcta. Supongamos que un estudiante sin preparación adecuada hace adivinanzas al azar y queremos calcular la probabilidad de que tenga exactamente tres respuestas correctas en las 4 preguntas.
- Con cuatro preguntas el examen, tenemos n=4
- Buscamos la probabilidad de exactamente 3 respuestas correctas, x=3
- La probabilidad de éxito (respuesta correcta para una pregunta es 0,2), entonces p=0,2
- La probabilidad de fracaso (respuesta incorrecta), es 0,8, entonces q=0,8
Este ejemplo cumple con las propiedades necesarias para ser una distribución binomial, que vamos utilizar la fórmula:
Entonces la cuenta queda: = (4). (0,008) . (0,8) = 0,0256
Recordamos que cuando hay 4! Tenemos que hacer 4x3x2x1. (TRIOLA, 2005)
3- DISTRIBUCIÓN DE POISSON
Es una distribución de probabilidad discreta. Expresa la probabilidad de un número k de eventos ocurriendo en un número fijo si estos eventos ocurren con una frecuencia media conocida y son independientes del tiempo discurrido desde el último evento. (RODRIGUEZ)
La variable aleatoria x es el número de ocurrencias de suceso en un intervalo. El intervalo puede ser tiempo, distancia, área, volumen o alguna unidad similar. (TRIOLA, 2005)
La fórmula utilizada es: donde e = 2,71828
Los requisitos para la distribución de Poisson: (TRIOLA, 2005)
- La variable aleatoria x es el número de ocurrencias de un suceso durante un intervalo
- Las ocurrencias deben ser aleatorias
- Las ocurrencias tienen que ser independientes entre sí
- Las ocurrencias deben estar uniformemente distribuidas dentro del intervalo que se emplea
La distribución de Poisson tiene los siguientes parámetros:
- La media es µ
- La desviación estándar es σ =
raíz cuadrada de µ
4-DISTRIBUCIÓN DE POISSON COMO APROXIMACIÓN DE LA BINOMIAL
Se utiliza cuando n es grande y p es pequeña, y hay que cumplir dos reglas:
- N>100
- Np<10
Si se cumplen dichas condiciones y deseamos utilizar la distribución de Poisson, como aproximación binomial, necesitamos un valor µ, ese valor se calcula utilizando: µ=np.
Bibliografia
Erick Cobo, P. M. (2007). Bioestadística para no estadísticos.
GLANTZ. (SEXTA EDICIÓN). BIOESTADISTICA.
Ricardi, F. Q. (2011). Distribución Normal. MEDWAVE.
RODRIGUEZ, M. R. (s.d.). IMPORTANCIA DE LA DISTRIBUCION BINOMIAL Y DE POISSON.
TAYLOR, B. Y. (s.d.). BIOESTADISTICA.
TRIOLA, M. F. (2005). ESTADISTICA. PEARSON.
WACKERLY, M. S. (SÉPTIMA EDICIÓN). ESTADÍSTICA MATEMÁTICA CON APLICACIONES.
¿Qué es el test de contraste de hipótesis? Todo lo que debo saber.
Existe un refrán galés originado en 1860 que dice: “Eat an apple on going to bed, and you’ll keep the doctor from earning his bread”. Esta frase ha sufrido modificaciones a lo largo del tiempo y es así como hoy en día se ha transformado en “An apple a day keeps the doctor away“. Si deseáramos adaptar todavía más esta frase al ámbito médico, podríamos simplemente cambiar la palabra «apple» por «aspirina»
De esta manera queda conformada una hipótesis; «Una aspirina al día mantiene al doctor en la lejanía». Pero… ¿Cómo podemos saber si esto realmente es así?, ¿Cómo sabemos si la hipótesis planteada es verdadera?, ¿De qué depende que una hipótesis se torne falsa?
La hipótesis y su problemática
Una hipótesis es algo que se supone como cierto o verdadero. Desde el punto de vista del Método Científico es una solución provisoria que aun no ha sido comprobada y que puede presentar distintos grados de fiabilidad. Una vez que esta queda verificada, pasa a ser un enunciado.
Las investigaciones que se realizan en el terreno de la medicina suelen ser del tipo comparativas. Es decir, se toman muestras poblacionales aleatorias y se analiza el efecto que producen los tratamientos en ellas. Su finalidad es observar qué tan efectivo es determinado fármaco o cómo responden los individuos a determinada terapia.
El problema que se nos plantea es si los resultados que obtenemos durante la investigación están dados por los efectos propios del fármaco o por alguna característica especial que pudieran llegar a tener los individuos de nuestra muestra tomada al azar.
Aquí es cuando entran en escena los Test de Contraste de Hipótesis y los errores asociados a ellos.
Test de Contraste de Hipótesis
También denominado prueba de significación; es un procedimiento basado en la evidencia de una muestra y en la teoría de probabilidades, usado para determinar si la hipótesis es una afirmación razonable.
En este test debemos enfrentar dos hipótesis opuestas formuladas al inicio del estudio. Una de ellas, la “suposición a favor”, es la hipótesis nula (H0). La hipótesis alternativa (H1) será la que se acepte cuando la hipótesis nula sea rechazada.
Si aplicamos esto a nuestro ejemplo, podemos establecer que:
- H0: «Una aspirina al día mantiene al doctor en la lejanía»
- H1: «Una aspirina al día NO mantiene al doctor en la lejanía» (o alguna hipótesis similar)
Durante la investigación siempre se empieza suponiendo que la H0 es verdadera. Se utilizarán los datos de la muestra para decidir si la evidencia está mas a favor de H0 o de H1. A partir de esto se obtiene una conclusión:
- Se acepta H0 y queda como verdadera
- Se rechaza H0 y queda como verdadera H1
La hipótesis nula se rechaza solo si los datos ofrecen suficiente evidencia para no considerarla verdadera
Pero aquí, volvemos a una de nuestras incógnitas iniciales.
El problema que se nos plantea es si los resultados que obtenemos durante la investigación están dados por los efectos propios del fármaco o por alguna característica especial que pudieran llegar a tener los individuos de nuestra muestra tomada al azar.
Se han realizado innumerables estudios sobre el efecto de la aspirina en los adultos mayores. Algunos llegan a la conclusión que la aspirina tiene un efecto favorable mientras que otros no solo no han visto ninguna mejoría en la salud, sino que ademas, aumenta el riesgo de hemorragias considerables (3).
Supongamos que se dispone de una población de 1.000 individuos y que para el estudio usaremos 5 muestras de 200 personas seleccionadas al azar. Los resultados no serán los mismos en todas las muestras al finalizar el estudio. Las diferencias se le van a atribuir al azar y no específicamente al fármaco que estemos probando, en este caso, la aspirina.
Entonces, ¿Cómo determinamos cuanta es suficiente evidencia?
Aquí entra en juego lo que se conoce como Nivel de Significancia, que es la probabilidad de rechazar la H0 cuando realmente es verdadera. En otras palabras, nos da un criterio para determinar si se tiene suficiente evidencia para descartar nuestra hipótesis nula. Un nivel de significancia aceptable varía entre 1 y 5%, ya que lo que menos queremos es que nuestra hipótesis nula sea rechazada cuando las probabilidades de ser verdadera son altas.
Al estar estudiando muestras y no una población entera, podemos cometer errores asociados a la aceptación o rechazo de la hipótesis nula. Se los conoce como errores alfa y beta.
- Error alfa o tipo 1: se comete cuando se rechaza una hipótesis que es correcta
- Error beta o tipo 2: se comete cuando se acepta una hipótesis que es incorrecta
Entonces; en el error alfa podemos decir que por causa del azar (patologías o condiciones de cada paciente) la aspirina no tiene ningún beneficio; y por otro lado, en el error beta y también por causa del azar (pacientes sin patologías) se acepta que la aspirina si es beneficiosa. En este ultimo caso, terminaríamos exponiendo a los pacientes a posibles hemorragias de gran calibre.
En definitiva, las pruebas de contraste de hipótesis intentan aceptar o rechazar una hipótesis nula, calculando la probabilidad de que los resultados obtenidos sean producto del azar. Gracias a ellas podemos calcular que tan probable es que en una investigación los resultados estén condicionados y determinados por el azar y que las diferencias que observamos sean debido a eso.
Referencias:
- Pruebas de contraste de hipótesis. Estimación puntual y por intervalos. Ágata Carreño Serra. SEDEN, Sociedad Española de Enfermería Nefrológica.
- Introducción a la probabilidad y estadística. Mendenhall, Beaver, Beaver. Cengage Learning. 2010. ISBN-13: 978-607-481-466-8
- Effect of Aspirin on Disability-free Survival in the Healthy Elderly. John J. McNeil, M.B., B.S., Ph.D., Robyn L. Woods, Ph.D., Mark R. Nelson, M.B., B.S., Ph.D. The New England Journal of Medicine DOI:10.1056/NEJMoa1800722
- Why an aspirin a day no longer keeps the doctor away …Marie Lordkipanidzé. University of Birmingham, Edgbaston, Birmingham, UK. doi: 10.1160/TH10-11-0749
¿Qué es el Poder Estadístico y cómo se calcula?
Objetivo
El objetivo de este artículo es reflejar conocimiento a futuros investigadores sobre la correcta recolección de datos, el uso correcto de los métodos estadísticos, conocer los modelos y métodos de cálculos y enfocar en la importancia del poder estadístico en los experimentos.
Introducción
Una de las herramientas más importantes y que no debe dejar de conocer en la realización de estudios e investigaciones es la estadística. Esta disciplina constituye un eje fundamental a la hora de recolectar y analizar datos experimentales brindando una respuesta racional a las grandes incertidumbres.
Aplicado a las ciencias de la salud, esta establece la medicina basada en la evidencia, donde demuestra la veracidad y eficacia de todas las investigaciones (ya sean antibióticos, vacunas, tratamientos, efectos adversos, etc.) pudiendo cambiar la manera en la que esta se ejerce y el empleo de sus recursos.
Al llegar a esta evidencia, puede que no sea la que el investigador quiso corroborar en una primera instancia. Muchos de los errores que cometen los investigadores están relacionados con la hipótesis formulada, el tamaño de la muestra, la población, la variabilidad, el diseño e incluso la calidad de esa misma evidencia.
Desarrollo
La Estadística se ocupa de reunir, clasificar, resumir, hallar regularidades, dar significado a las diferencias observadas, y analizar los datos aleatorios; siempre y cuando la variabilidad e incertidumbre sea una causa intrínseca de los mismos, con el fin de ayudar a la toma de decisiones y formular predicciones.
Al reunir los datos necesarios para realizar su propia investigación, se tienen que tomar en cuenta diversos puntos, siendo la más importante la correcta delimitación del campo de estudio sobre su población d interés. Por lo general los experimentos se realizan tomando dos muestras aleatorias de un grupo población. (Un grupo A y un grupo B).
Una vez definida la muestra poblacional, es fundamental entender el uso y análisis del poder estadístico. Este término hace referencia a la probabilidad de rechazar una hipótesis nula.
La probabilidad de rechazar una hipótesis nula cuando es realmente falsa se representa como β.
Poder estadístico= 1 – β
Al comenzar, el investigador tiene que realizar dos tipos de hipótesis.
Una hipótesis la cual se llama hipótesis alternativa (H1= hipótesis que afirma el resultado al que se quiere concluir en la investigación), y paralelamente genera la hipótesis nula (H0= afirmación contraria a la que quiere llegar el investigador).
Cuando la hipótesis da como resultado que es no significativa, el poder estadístico revisa si realmente esta hipótesis no tiene impacto o efecto, o el problema no es la hipótesis sino otro factor, como el tamaño muestral. Este poder evita conclusiones falsas y mejora la interpretación de los resultados.
En el experimento de esta investigación, donde ya comentamos que se van a utilizar dos grupos, la H0 más común indica que no hay diferencia entre las poblaciones A y B. En cambio, la H1 afirma que hay diferencia, pudiendo esta demostrar por ejemplo la diferencia de un mismo tratamiento, afectos adversos o positivos en dos grupos diferentes.
Cuando las hipótesis estén definidas y los datos se hayan obtenido correctamente, el investigador decidirá si hay suficiente evidencia para rechazar la hipótesis nula.
Para no cometer ninguno de estos errores, se tiene que tener un alto poder estadístico. Si se tiene poco poder estadístico no se podrán detectar pequeñas diferencias entre los grupos poblacionales, generando una gran debilidad en el diseño de la investigación.
Cálculo
El poder estadístico (1- β) se calcula con la utilización de la siguiente formula(6):

Donde:
- ∆ = Diferencia entre la media de los grupos.
- Ơ = Desviación estándar conjunta.
- nT y nC = Tamaños de las muestras de cada grupo.
Para ver ejemplificado el uso de la formula Z, dejo citado este video para que demuestre el correcto cálculo del poder estadístico(10).
Conclusión
El análisis de poder estadístico es una herramienta indispensable en la realización de investigaciones ya que detecta el impacto de la investigación, permitiendo calcular el diseño, la metodología, efectos y errores de los datos siendo el tamaño muestral su principal determinante.
Puede tener múltiples resultados ya sea que la hipótesis nula sea verdadera, sea falsa, sea falsa y rechazada, o sea verdadera y rechazada.
Podemos concluir que(9):
- A mayor muestra, más poder.
- A menor efecto, se requiere mayor tamaño muestral.
- A mayor variabilidad en la población, se requiere mayor tamaño muestral.
- A menor significancia estadística, menor poder de la prueba.
Si el poder estadístico es pobre, la investigación no llegará a conclusiones firmes, su resultado será sospechoso y muy factible a sesgos.
Referencias
1. Biostatistics for the health sciences (2008), Primera edición, de R. Clifford Blair y Richard A. Taylor, publicada originalmente en inglés por Pearson Education Inc., publicada como PRENTICE HALL INC.
2. Bioingenieria e Informatica Médica. Curso: Bioestadística básica para médicos asistenciales. Cuarto Congreso Virtual de Cardiología. Septiembre 2005
3. Bioéstadística: Métodos y Aplicaciones U.D. Bioestadística. Facultad de Medicina. Universidad de Málaga. ISBN: 847496-653-1
4. Primer of Biostatistics (Glantz)(Paperback) McGraw-Hill Medical; Edición: 6 (15 de abril de 2005) ISBN-10: 0071435093 ISBN-13: 978-0071435093
5. Andrew D. Althouse, PhD Pittsburgh, PA 5 de agosto de 2015 Lenth RV. Poder post hoc: tablas y comentarios. Disponibleen: http: //www.stat.uiowa. edu / fi les / stat / techrep /tr378.pdf . Consultado el 4 de agosto de 2015. http://dx.doi.org/10.1016/j.amjcard.2015.09.013
6. Gesto Giannattasio, Nora. (2016). Análisis de Poder Estadístico y su Aplicación a Evaluaciones Experimentales. DOI: 10.13140/RG.2.1.1545.7366.
7. Introducción a la inferencia estadística. Armando Aguilar Marquéz, Jorge Altamira Ibarra, Omar García León, Profesores del departamento de Matemáticas, Facultad de Estudios Superiores Cuautitlán, UNAM.
8. Introducción a la inferencia estadística. PEARSON EDUCACIÓN, México, 2010 ISBN: 978-607-442-737-0. PRIMERA EDICIÓN
9. https://www.youtube.com/watch?v=_BHJGWfksjw
10. https://www.youtube.com/watch?v=rbpgjMABhV8
¿Qué es la Precisión y la Exactitud? ¿Para qué se utilizan? ¿Cómo se calculan?
Objetivo Educativo:
Este artículo tiene el objetivo de ayudar al alumno que necesite hacer un trabajo de final de carrera a entender los criterios relacionados con la exactitud y la precisión de un instrumento de medición , a fin de reducir los sesgos y promover mayor confiabilidad y validez de su estudio. En un trabajo de investigación, la integridad de los datos depende de la integridad del sistema de medición.
La precisión y la exactitud son términos que están relacionados entre si y que se refieren a la capacidad que tiene un instrumento o escala al momento de la medición de las variables. La medición tendrá mayor validez mientras más precisa y exacta sea. Si se obtiene resultados con poca variabilidad con un instrumento, se presume que este es más preciso. Ya la exactitud de un instrumento se relaciona a capacidad de obtener resultados verdaderos y libres de sesgos. (1)
La precisión en un estudio y su utilidad
Por definición la precisión es la cercanía de dos o más valores de varias mediciones entre sí. Hay más precisión mientras más cerca estén los valores de diferentes mediciones y eso tiene una grande influencia en la potencia de un estudio porque mientras más precisa sea la medida, mayor será la potencia estadística, o sea, la precisión aumenta la potencia para detectar defectos. (2)
La palabra clave aquí es reproducibilidad. Es así que se valora la precisión, con la reproducibilidad de mediciones repetidas y esto está relacionado con los llamados errores aleatorios. Algunas fuentes de errores aleatorios son: (3)
- Variabilidad del observador (incluye factores como escoger palabras en una entrevista o tener habilidad para usar un instrumento mecánico) (3)
- Variabilidad del sujeto (se debe a la variabilidad biológica intrínseca de los participantes en el estudio) (3)
- Variabilidad del instrumento (incluye factores ambientales cambiantes, el desgaste de los componentes mecánicos, entre otros) (3)
Un instrumento es confiable y preciso cuando las mediciones realizadas generen los mismos resultados en diferentes momentos, escenarios y poblaciones. Pero en la practica la confiabilidad se conjuga con otro concepto que es la validez, dando origen a diversos escenarios, desde mediciones válidas y confiables hasta aquellas que carecen de validez y de confiabilidad. (2)
Unos de los principios fundamentales de la precisión en un estudio es la confiabilidad, o consistencia de las mediciones. És necesario que los investigadores intenten reducir la cantidad de fuentes de potenciales errores relacionados con la medición de las variables para proporcionar una mayor confianza en los resultados. (2)
Existen cinco métodos que se pueden emplear para tratar de reducir al mínimo el error aleatorio y aumentar la precisión de las determinaciones de cualquier estudio: la normalización de los métodos de medida, la formación y certificación de los observadores, el perfeccionamiento de los instrumentos, la automatización de los instrumentos y por último, repetir las determinaciones. (5)
Para cada una de las mediciones del estudio, es el investigador que decide cuánto hincapié debe hacer en cada una de estas estrategias.
Como se calcula la precisión de un estudio
Se calcula a través de la proporción de verdaderos positivos contra todos los resultados positivos, tanto verdaderos positivos (VP), como falsos positivos (FP): (3)
La fórmula és:
Precision = VP/VP+FP
Ahora, cuando es necesario estimar la precisión de una población (estadísticos), esta se calcula a través de un intervalo de confianza (IC). (4)
IC es una medida de la precisión de los resultados de un estudio con la finalidad de establecer inferencias sobre la población estudiada. En ciencias de la salud se suele utilizar un intervalo de confianza de 95%, debido a que sólo es posible aceptar como máximo un 5% de error estándar en las afirmaciones. (4)
La fórmula del IC se compone de dos parámetros principales; el primero denominado (d ), diferencia entre dos medidas (proporciones, medias, medianas, entre otras) y (e ), el error estándar aceptado para esa diferencia bajo una curva normal con un valor de Z= 1.96. (4)
Por lo tanto, la fórmula en general és [d +/- 1.96(e)].
Para lo cual, el error estándar se obtiene mediante 2√p (1-p)/n, donde “p” representa a la proporción de sujetos con el evento estudiado y (1-p) a la diferencia de la unidad menos el valor de “p” que se divide entre el número de pacientes. (4)
Siempre que se trate de estudios donde se analicen diferencias entre dos o más grupos para medias, proporciones (%), riesgos relativos y también para calcular estimaciones de estudios de diagnóstico (sensibilidad, especificidad, valores predictivos positivos e índices de probabilidad), tratamiento, casos y controles, inclusive meta análisis, es necesario incluir el IC. (4)
Exactitud y su utilidad
Exactitud en una prueba diagnóstica se refiere al grado en que sus resultados coinciden con un parámetro de referencia claro y objetivo, o sea, la exactitud de una variable es el grado en que representa el valor verdadero y su utilidad para un estudio es aumentar la validez de las conclusiones. (4)
En las ciencias de la salud, se dice que la exactitud és la capacidad de una prueba diagnóstica para clasificar correctamente a los individuos en subgrupos clínicamente relevantes (enfermos y NO enfermos)”. (5)
La exactitud va a depender del error sistemático (sesgo); cuanto mayor sea el error, menos exacta será la variable. Los posibles sesgos son: (4)
Sesgo del observador: una deformación, consciente o inconsciente de la percepción o la notificación de la medida por el observador. (4)
Sesgo del instrumento: funcionamiento defectuoso de un instrumento mecánico. (4)
Sesgo del participante: la deformación de la medición por parte del participante en el estudio, por ejemplo, al notificar un suceso (sesgo de respuesta o de recuerdo). (4)
Como se calcula la exactitud en un estudio
A diferencia de la precisión, la exactitud de una medición se evalúa mejor comparándola (si posible) con algún criterio de referencia. (4)
De manera práctica, se calcula con la proporción de resultados verdaderos (positivos y negativos) entre el número total de casos examinados (verdaderos positivos, falsos positivos, verdaderos negativos, falsos negativos). Por lo tanto, la formula es: (5)
Exactitud= VP+VN/VP+FP+FN+VN
Para incrementar la exactitud de un estudio también es posible contar con estrategias parecidas a las utilizadas para determinar la precisión: normalización de los métodos de medición, formación y certificación de los observadores, perfeccionamiento de los instrumentos, automatización de los instrumentos, realización de medidas que no se perciban (es posible diseñar mediciones de las que no sea consciente el participante y así eliminar la posibilidad de que conscientemente introduzca sesgo en la variable), calibración del instrumento y enmascaramiento. (5)
La decisión del interés que se debe poner en aplicar cada una de estas estrategias, así como en el caso de la precisión, es del elección del investigador.
Referencias:
- Villasís-Keever MÁ, Márquez-González H, Zurita-Cruz JN, Miranda-Novales G, Escamilla-Núñez A. El protocolo de investigación VII. Validez y confi abilidad de las mediciones. Rev Alerg Mex. 2018;65(4):414-421
- Manterola, Carlos, Grande, Luis, Otzen, Tamara, García, Nayely, Salazar, Paulina, & Quiroz, Guissela. (2018). Confiabilidad, precisión o reproducibilidad de las mediciones. Métodos de valoración, utilidad y aplicaciones en la práctica clínica. Revista chilena de infectología, 35(6), 680-688. https://dx.doi.org/10.4067/S0716-10182018000600680
- Portillo, Jacobo Diaz. Guía Práctica del Curso de Bioestadística Aplicada las Ciencias de la Salud. Alcalá, Madrid: Instituto Nacional de Gestión Sanitaria.
- Arceo Díaz, José LuisManual de medicina basada en evidencias / José LuisArceo Diaz, José Manuel Ornelas Aguirre, Susana Dominguez Salcido. México : Editorial El Manual Moderno, 2010. xii, 192 p. : il. ; 23 cm. Incluye índice ISBN 978-607-448-054-2
- Hulley SB, Cummings SR. Planificación de las mediciones: precisión y exactitud. En: Diseño de la investigación clínica. Barcelona: Doyma, 1993; 35-46.
¿Qué es la prueba estadística T de student? ¿Para qué sirve? ¿Cómo se Calcula? ¿Cómo se interpreta?
Objetivo educativo:
Este artículo tiene como objetivo presentar a los alumnos de medicina sobre la prueba T de student, que puedan entender de manera práctica como interpretarlo y utilizarlo para sus trabajos de investigación a futuro.
Introducción:
La prueba T de student es una prueba de hipótesis de medias en la cual se usa la distribución T. El objetivo es plantear correctamente la prueba y distribución T. Esta distribución es un conjunto de curvas estructurada por un grupo de datos de unas muestras en particular. Permite comparar dos muestras de tamaño menor o igual a 30. Esta prueba se usa con frecuencia en las publicaciones médicas y cabe destacar que es el procedimiento estadístico más usado. (1)
Clasificación:
Se puede clasificar según el tipo de muestra:
-Pruebas T de student para muestras independientes: Hipótesis sobre los valores de dos muestras obtenidas de dos poblaciones totalmente independientes. Los objetivos son la normalidad, homogeneidad de varianzas y la independencia. (5)
Ejemplo: se evalúa el efecto de un tratamiento médico, y se recluta a 100 personas para el estudio. Luego se elige aleatoriamente 50 sujetos para el grupo en tratamiento y 50 sujetos para el grupo de control. En este caso, obtenemos dos muestras independientes y podríamos utilizar la forma desapareada de la prueba t.
-Pruebas T de student para muestras relacionadas: Hipótesis sobre los valores de dos muestras relacionadas, solo hay un grupo de personas pero se las mide dos veces. El objetivo es la normalidad.
Ejemplo: personas evaluadas antes y después de un tratamiento.
-Pruebas T de student para una muestra: Hipótesis sobre los valores de las medias poblacionales, es decir, se compara los resultados de una muestra con un valor existente en la bibliografía.
Diferencias:

- La distribución t student es menor en la media y más alta en los extremos que una distribución normal.
- Tiene proporcionalmente mayor parte de su área en los extremos que la distribución normal.
Características:
- Para realizar una prueba T de student se requiere una media muestral (x̄), una media poblacional (µ) y un error estándar (SE). (4)
- El error estándar se calcula:

- Se utiliza para comparar dos medias de poblaciones independientes y normales, determinando de si hay alguna diferencia significativa entre las medias de dos grupos.
- Errores tipo I y II: En el contraste de hipótesis hay dos tipos de errores, el error tipo I es aquella que toma la acción alternativa cuando la hipótesis nula era cierta, y el error tipo II es aquella que toma la acción nula cuando la hipótesis alternativa era cierta.
Las probabilidades correspondientes de cometer errores tipo I y II reciben el nombre de riesgos α y β :
-Riesgo α = P (tomar la acción alternativa cuando es cierta la hipótesis nula)
-Riesgo β = P (tomar la acción nula cuando es cierta la hipótesis alternativa)
Ejemplo:
Riesgo α = P (Decidir es una B cuando en realidad es un 8)
Riesgo β = P (Decidir es un 8 cuando en realidad es una B)
De esta manera, α representa la proporción de 8 que serán
identificados como B y β su recíproco. (2)
Metodología:
- Probar que cada una de las muestras tenga una distribución normal.
- Obtener para cada una de las muestras: el tamaño de las muestras (n1 y n2), sus respectivas medias (m1 y m2) y sus varianzas (v1 y v2).
- Probar que las varianzas sean homogéneas.
- En caso de homogeneidad en esas varianzas: establecer la diferencia entre las medias (m1-m2), y calcular la varianza común de las dos muestras.
VC= (n1-1) v1 + (n2-1) v2 / (n1 + n2 – 2)
Es decir, la varianza común (VC) es igual a un promedio pesado de las varianzas de las dos muestras en donde los pesos para ese promedio son iguales al tamaño, menos uno (n – 1) para cada una de las muestras. Con esta varianza se calcula el error estándar de la diferencia de las medias (ESM).
ESM= ((vc) (n1 + n2) / (n1 n2))
- Por último, la T-student es igual al cociente de la diferencia de medias entre el ESM anterior. (8)
Pasos a seguir:
- El primer paso de importancia es declarar la hipótesis: la hipótesis nula (Ho) es cuando las medias de dos muestras son iguales, en cambio, la hipótesis alternativa (H1) es cuando las medias de las dos muestras son diferentes. (3)
- El segundo paso es:
- El nivel de significancia(α): es el área de rechazo, es decir es la probabilidad de rechazar la hipótesis nula cuando esta es verdadera. Si n es menor a 100, α es de 5%. En cambio, si n es mayor a 100, α es de 1% (más estricto). Se considera un nivel alfa de: 0.05 para proyectos de investigación; 0.01 para aseguramiento de la calidad; y 0.10 para estudios o encuestas de mercadotecnia. Pruebas de significación pueden ser bilaterales (dos colas) o unilaterales (una cola). Las bilaterales contemplan los casos en contra de H en ambas colas. Por otro lado, las unilaterales por la derecha contemplan los casos en contra de H en el lado derecho, en cambio, las unilaterales por al izquierda contemplan los casos en contra de H en el lado izquierdo. (1)
- Grados de libertad (gl): es el número determinado para saber la variabilidad de eventos de una muestra. Es el número de valores que se puede elegir libremente, existiendo un total fijo. Si el tamaño de la muestra aumenta, habrá un aumento sobre la información de la población, y por lo tanto, habrá un aumento de los grados de libertad de los datos. GL= n-1 (si es una muestra); GL=(n1+n2)-2 (si son dos muestras). (6)
- Puntos críticos: se obtiene de la tabla de variación de donde hay columnas del nivel de significancia contra los renglones de los grados de libertad. El número que se cruza es el punto crítico.
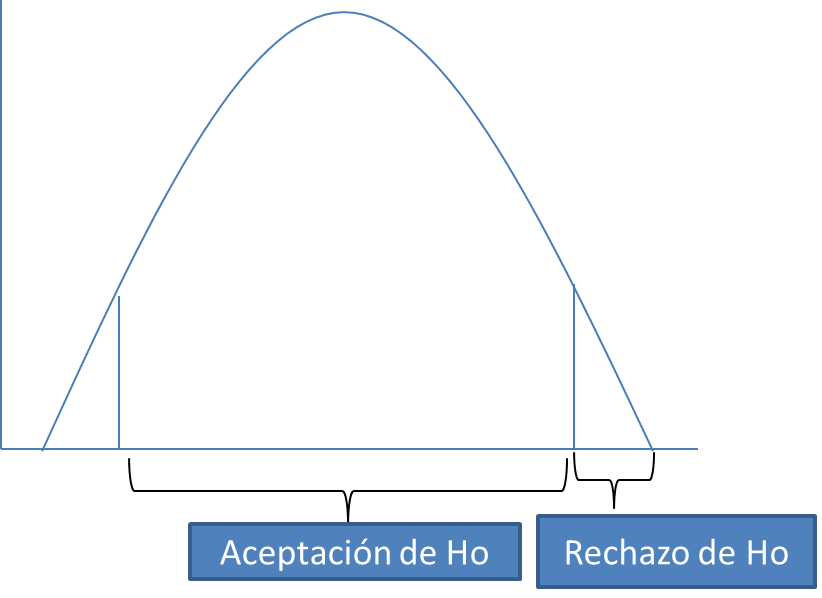
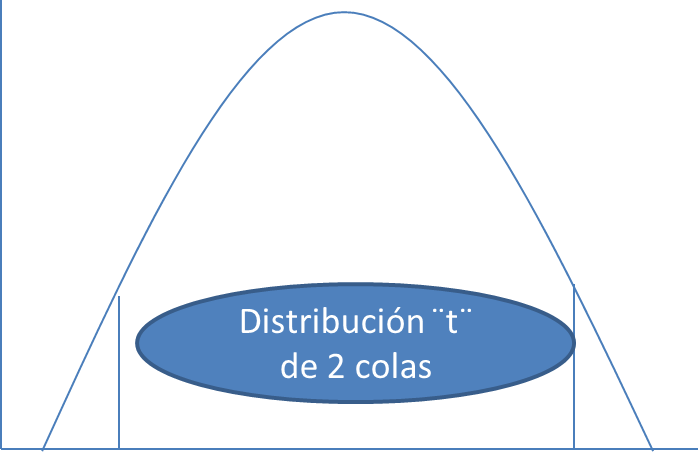

- El tercer paso es conseguir el punto de prueba T:
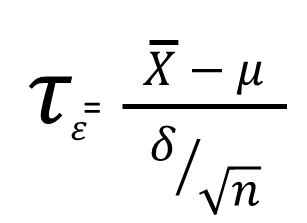
- El cuarto paso es comparar el punto de prueba:



- Valor de P: Indica la confiabilidad que nos da la diferencia para poder rechazar la hipótesis nula. Si P es menor a α se rechaza la hipótesis nula. En cambio, si P es mayor a α se acepta la hipótesis nula. (2)
Referencias:
- (1). Stanton, A. (2005). Bioestadística: ¨El caso especial de dos grupos: la prueba T¨. México. file:///C:/Users/Sony%20Vaio/Desktop/tesis/Bioestadistica%20Glantz_booksmedicos.org.pdf
- (2). Cobo, E., Muñoz, P., González, J. (2007). Bioestadística para no estadísticos: bases para interpretar artículos científicos. España. file:///C:/Users/Sony%20Vaio/Desktop/tesis/Bioestadistica.para.no.estadisticos.pdf
- (3). Spiegel, M., Stephens, L. (2009). Estadística: Schaum. México: Instituto tecnológico y de estudio superior de Monterrey. file:///C:/Users/Sony%20Vaio/Desktop/tesis/Estadistica.Spiegel.pdf
- (4). Roldán, L. Prueba T student. Universidad Rafael Landívar. https://www.youtube.com/watch?v=ekf208Fvzcw
- (5). Serra, P. T de student: Muestras independientes. Universidad de Valencia. https://www.youtube.com/watch?v=lyhtl2eoV-8&t=72s
- (6) Soporte de minitab. Qué son los grados de libertad. https://support.minitab.com/es-mx/minitab/18/help-and-how-to/statistics/basic-statistics/supporting-topics/tests-of-means/what-are-degrees-of-freedom/
- (7) https://es.wikiversity.org/wiki/Prueba_de_hip%C3%B3tesis_(estad%C3%ADstica)
- (8) By student. (1908). The probable error of a mean: Biometrika.
Medidas de dispersión
Al finalizar este artículo vamos a entender que, aunque la veamos muy alejada, la estadística esta mas cerca de lo que pensamos. Es que sin ella veríamos conjuntos de datos sin sentido.
Vamos a conocer sobre las diferentes medidas de variabilidad de los datos: una manera de resumir los resultados y poder obtener conclusiones sobre lo general, aun cuando no conocemos toda la información.
Seguí leyendo “Medidas de dispersión”