Publicado el por grecco karen yamila

¿Qué es la prueba estadística T de student? ¿Para qué sirve? ¿Cómo se Calcula? ¿Cómo se interpreta?

Objetivo educativo:

Este artículo tiene como objetivo presentar a los alumnos de medicina sobre la prueba T de student, que puedan entender de manera práctica como interpretarlo y utilizarlo para sus trabajos de investigación a futuro.

Introducción:

La prueba T de student es una prueba de hipótesis de medias en la cual se usa la distribución T. El objetivo es plantear correctamente la prueba y distribución T. Esta distribución es un conjunto de curvas estructurada por un grupo de datos de unas muestras en particular. Permite comparar dos muestras de tamaño menor o igual a 30. Esta prueba se usa con frecuencia en las publicaciones médicas y cabe destacar que es el procedimiento estadístico más usado. (1)

Clasificación:

Se puede clasificar según el tipo de muestra:

-Pruebas T de student para muestras independientes: Hipótesis sobre los valores de dos muestras obtenidas de dos poblaciones totalmente independientes. Los objetivos son la normalidad, homogeneidad de varianzas y la independencia. (5)

Ejemplo: se evalúa el efecto de un tratamiento médico, y se recluta a 100 personas para el estudio. Luego se elige aleatoriamente 50 sujetos para el grupo en tratamiento y 50 sujetos para el grupo de control. En este caso, obtenemos dos muestras independientes y podríamos utilizar la forma desapareada de la prueba t.

-Pruebas T de student para muestras relacionadas: Hipótesis sobre los valores de dos muestras relacionadas, solo hay un grupo de personas pero se las mide dos veces. El objetivo es la normalidad.

Ejemplo: personas evaluadas antes y después de un tratamiento.

-Pruebas T de student para una muestra: Hipótesis sobre los valores de las medias poblacionales, es decir, se compara los resultados de una muestra con un valor existente en la bibliografía.

Diferencias:

O. Distribución T de Student - Procesamiento de Información ...
  • La distribución t student es menor en la media y más alta en los extremos que una distribución normal.
  • Tiene proporcionalmente mayor parte de su área en los extremos que la distribución normal.

Características:

  • Para realizar una prueba T de student se requiere una media muestral (x̄), una media poblacional (µ) y un error estándar (SE). (4)
  • El error estándar se calcula:
  • Se utiliza para comparar dos medias de poblaciones independientes y normales, determinando de si hay alguna diferencia significativa entre las medias de dos grupos.
  • Errores tipo I y II: En el contraste de hipótesis hay dos tipos de errores, el error tipo I es aquella que toma la acción alternativa cuando la hipótesis nula era cierta, y el error tipo II es aquella que toma la acción nula cuando la hipótesis alternativa era cierta.

Las probabilidades correspondientes de cometer errores tipo I y II reciben el nombre de riesgos α y β :

-Riesgo α = P (tomar la acción alternativa cuando es cierta la hipótesis nula)

-Riesgo β = P (tomar la acción nula cuando es cierta la hipótesis alternativa)

Ejemplo:

Riesgo α = P (Decidir es una B cuando en realidad es un 8)
Riesgo β = P (Decidir es un 8 cuando en realidad es una B)

De esta manera, α representa la proporción de 8 que serán
identificados como B y β su recíproco. (2)

Metodología:

  1. Probar que cada una de las muestras tenga una distribución normal.
  2. Obtener para cada una de las muestras: el tamaño de las muestras (n1 y n2), sus respectivas medias (m1 y m2) y sus varianzas (v1 y v2).
  3. Probar que las varianzas sean homogéneas.
  4. En caso de homogeneidad en esas varianzas: establecer la diferencia entre las medias (m1-m2), y calcular la varianza común de las dos muestras.

VC= (n1-1) v1 + (n2-1) v2 / (n1 + n2 – 2)

Es decir, la varianza común (VC) es igual a un promedio pesado de las varianzas de las dos muestras en donde los pesos para ese promedio son iguales al tamaño, menos uno (n – 1) para cada una de las muestras. Con esta varianza se calcula el error estándar de la diferencia de las medias (ESM).

ESM= ((vc) (n1 + n2) / (n1 n2))

  • Por último, la T-student es igual al cociente de la diferencia de medias entre el ESM anterior. (8)

Pasos a seguir:

  • El primer paso de importancia es declarar la hipótesis: la hipótesis nula (Ho) es cuando las medias de dos muestras son iguales, en cambio, la hipótesis alternativa (H1) es cuando las medias de las dos muestras son diferentes. (3)
  • El segundo paso es:
  1. El nivel de significancia(α): es el área de rechazo, es decir es la probabilidad de rechazar la hipótesis nula cuando esta es verdadera. Si n es menor a 100, α es de 5%. En cambio, si n es mayor a 100, α es de 1% (más estricto). Se considera un nivel alfa de: 0.05 para proyectos de investigación; 0.01 para aseguramiento de la calidad; y 0.10 para estudios o encuestas de mercadotecnia. Pruebas de significación pueden ser bilaterales (dos colas) o unilaterales (una cola). Las bilaterales contemplan los casos en contra de H en ambas colas. Por otro lado, las unilaterales por la derecha contemplan los casos en contra de H en el lado derecho, en cambio, las unilaterales por al izquierda contemplan los casos en contra de H en el lado izquierdo. (1)
  2. Grados de libertad (gl): es el número determinado para saber la variabilidad de eventos de una muestra. Es el número de valores que se puede elegir libremente, existiendo un total fijo. Si el tamaño de la muestra aumenta, habrá un aumento sobre la información de la población, y por lo tanto, habrá un aumento de los grados de libertad de los datos. GL= n-1 (si es una muestra); GL=(n1+n2)-2 (si son dos muestras). (6)
  3. Puntos críticos: se obtiene de la tabla de variación de donde hay columnas del nivel de significancia contra los renglones de los grados de libertad. El número que se cruza es el punto crítico.
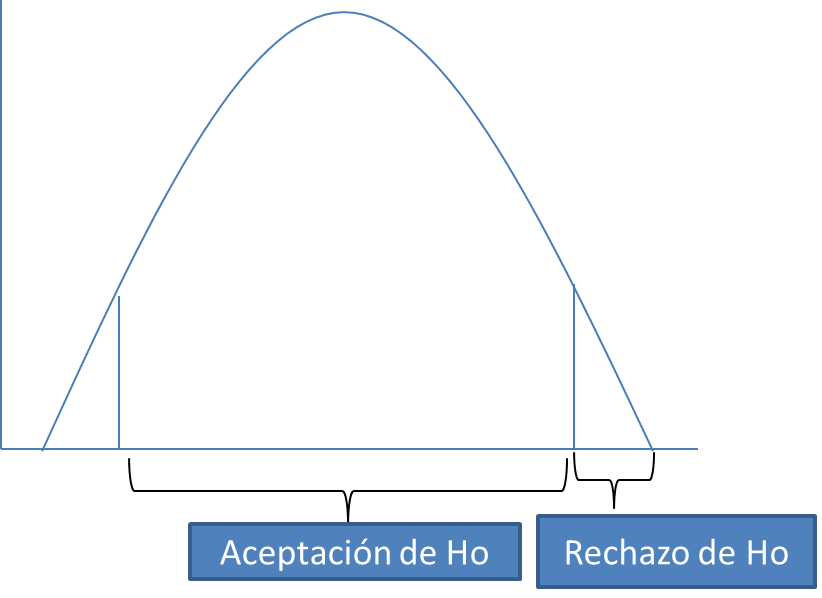
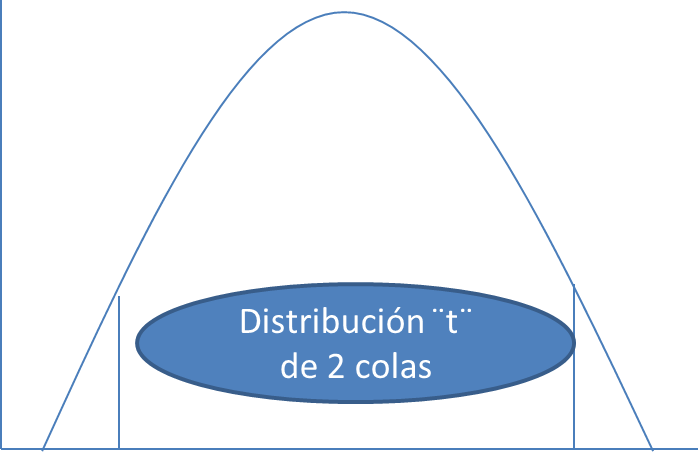
  • El tercer paso es conseguir el punto de prueba T:
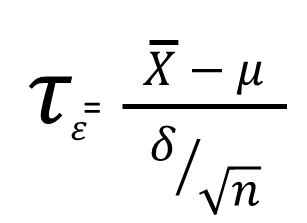
  • El cuarto paso es comparar el punto de prueba:
Prueba de hipótesis (estadística) - Wikiversidad
Cuando la H1 es diferente.
Área de aceptación y rechazo menor
Cuando H1 es menor.
Área de aceptación y rechazo mayor
Cuando H1 es mayor. (7)
  • Valor de P: Indica la confiabilidad que nos da la diferencia para poder rechazar la hipótesis nula. Si P es menor a α se rechaza la hipótesis nula. En cambio, si P es mayor a α se acepta la hipótesis nula. (2)

Referencias:

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *