La prueba de McNemar es útil para comparar dos muestras que se relacionan o emparejan, con aplicación a diseños del tipo “antes y después. (1) Es una herramienta estadística importante para decidir si es aceptable determinado tratamiento o diagnostico. Puede ser útil para estudios pareados de sensibilidad y especificidad. (2) En este trabajo demostraremos la utilidad, las herramientas para que se emplee y las interpretaciones de esta prueba.
Desarrollo del tema:
La prueba de McNemar se clasifica como una prueba “no paramétrica”, cuya utilización es basada en una hipótesis a lo cual no hay organización de los datos. En esta prueba se compara la respuesta binaria para los datos de pares coincidentes. (5)
¿Para qué sirve la prueba de McNemar?
La prueba de McNemar es utilizada para comprobar la homogeneidad marginal para resultados binarios correlacionados. Sirve para evidenciar hipótesis sobre proporciones iguales. Se pude utilizar esta prueba para comparar al mismo sujeto dos veces antes y después del tratamiento, o también se puede utilizar en comparaciones de pruebas diagnóstico.(3)(2)
¿Cómo se Calcula la prueba de McNemar?
Para calcular la prueba de McNemar se dispone una tabla de contingencia 2 x 2 para buscar el conjunto de las respuestas de los mismo elementos antes y después.(4)
| Antes/Después | – | + |
| – | A | B |
| + | C | D |
En la tabla,
- A es el nº de elementos que continúan “-“.
- B es el nº de elementos que cambiaron de “-” a “+”.
- C es el nº de elementos que cambiaron de “+” a “-“.
- D es el nº de elementos que continúan “+”.
Las hipótesis estadisticas son,
H1 (alterna) = cambios derivados del tratamiento
Cuando H1 es verdadero, el estadístico de que permite contrastar si hay diferencias entre las frecuencias observadas es (1):
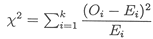
- Oi= frecuencia observada en la i-ésima celda
- Ei = frecuencia esperada en la i-ésima celda si H0 es cierta
- k = número de celdas
A lo cual se interesan solamente las celdas que ocurren cambios y puede constatar la significación de los cambios a través del estadístico (1):
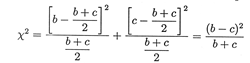
Ho (nula) = cambios al azar
Cuando H0 es verdadero, el valor de X² hace referencia a la distribución de chi-cuadrado con un grado de libertad. La formula estadística es (4):
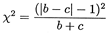
¿Cómo se interpreta la prueba de McNemar?
Los resultados son interpretados a través de contraste de hipótesis, utilizando tablas de distribución chi-cuadrado y tabla la tabla de distribución binominal. Es posible hacer uso del software SPSS.(3)(1)
El contraste se interpreta de la siguiente manera, en caso de que C sea menor que B, la hipótesis nula es que C es un valor de una variable X con distribución binominal de parámetros n= B+C y π= 0,5. El nivel de significación para una prueba de dos colas es P( X < C ) + P( X > B) y se rechaza la hipótesis nula para niveles de significación iguales o superiores. Si la hipótesis alternativa es direccional el nivel de significación a partir del cual se rechaza la hipótesis nula es la mitad del nivel de significación bilateral. (1)
Link de las tablas:
X²: https://drive.google.com/file/d/0B0HQjA3-vWRmUTl1OXNhTzJvaFE/view
Binomial: https://drive.google.com/file/d/0B0HQjA3-vWRmdjRWMGxQbFU1NDA/view
Como ejemplo ilustrativo sigue abajo en anexo un video practico:
Referencias:
1. (No Title) [Internet]. [cited 2020 Apr 30]. Available from: http://www.ub.edu/aplica_infor/spss/cap6-3.htm
2. Kim S, Lee W. Does McNemar’s test compare the sensitivities and specificities of two diagnostic tests? Stat Methods Med Res. 2017;26(1):142–54.
3. Silvente VB, Hurtado R. Classificació de proves no paramètriques. Com aplicar-les en SPSS. Rev d’Innovació i Recer en Educ. 2012;5(2):101–13.
4. Altman DG. PRACTICAL STATISTICS FOR MEDICAL The Analysis of Time Series. 1997. 277-300. p.
5. Hernández-Sampieri R, Mendoza Torres C. Metodología de la investigación. Ciudad de México: McGraw-Hill Interamericana; 2018.