Objetivo educativo:

El objetivo de este trabajo es adquirir conocimiento acerca de una parte de la bioestadística que es la distribución muestral, que habla de hacer cuentas de probabilidad, a partir de una parte de la población, visando entender que es una población, una muestra, un muestreo y saber la diferencia entre los tipos de distribución y saber cuándo utilizarlas.

Desarrollo del tema:

¿QUE ES UNA DISTRIBUCIÓN MUESTRAL?

Es una parte de la estadística que es necesario su compresión para desenvolver herramientas metodológicas, como para hacer estudios de una determinada muestra, en una determinada población haciendo y trabajando con probabilidades.

                Una distribución muestral es una distribución de muestras estadísticas que se obtienen, por lo regular, de una o más poblaciones. (TAYLOR)

                Para hacer una distribución muestral, necesito un muestreo que es una técnica de selección a partir de una población de una muestra; que se va considerar todas las muestras posibles para una determinada población. A partir de estas muestras se calcula la probabilidad, y también se puede estimar el error para la muestra. La muestra se toma de manera aleatoria, sea una muestra simple o compleja, para evitar los sesgos que es la diferencia sistemática entre las características de los miembros de la muestra y la población de la que se obtuvo. (GLANTZ, SEXTA EDICIÓN)

                La elaboración de una distribución va depender de: una población que va tener datos que van generar un parámetro µ o p, y va depender de una muestra que va generar un estadístico x o p, donde la población es la totalidad de elementos que interesa estudiar, normalmente no es estudiada toda la población; el muestreo que es parte de la población que ha de estudiarse, con el objetivo de tener resultados generalizados a toda la población y una muestra que tiene que ser de características similares de la población completa a fin de que sea representativa.

Cuando hablamos de las distribuciones muestrales vamos a tener dos clasificaciones, donde una variable aleatoria significa que tiene un numero único y es determinado al azar, en cuanto una variable aleatoria discreta tiene un número finito de valores y la continua un número infinito de valores.

1. Distribución de Variables Aleatorias Discretas: Binomial, Poisson, Hipergeométrica
2. Distribución de Variables Aleatorias Continuas: Normal

1. DISTRIBUCIÓN NORMAL

                Es utilizado para representar la distribución de variables cuantitativas, o sea, tiene un infinito de valores. Este tipo de distribución tiene la conocida forma de campana o montaña, y para hacer una distribución normal es necesario la determinación de los parámetros:

• Media (µ) que representa el centro de gravedad, es decir, aquel punto que permitirá aguantar en equilibrio, la distribución. (Bioestadística para no estadísticos)
• Desviación típica (σ) es la distancia con la media del punto de máxima pendiente (Bioestadística para no estadísticos).
• Es una distribución simétrica.
• Es asintótica, es decir sus extremos nunca tocan el eje horizontal, cuyos valores tienden a infinito.
• En el centro de la curva se encuentran la media, la mediana y la moda.
• El área total bajo la curva representa el 100% de los casos.
• Los elementos centrales del modelo son la media y la varianza. (Ricardi, 2011)
• Representación gráfica

Se dice que muchos fenómenos en el campo de la salud se distribuyen normalmente. Esto significa que si uno toma al azar un número suficientemente grande de casos y construye un polígono de frecuencias con alguna variable continua, por ejemplo peso, talla, presión arterial o temperatura, se obtendrá una curva de características particulares, llamada distribución normal. Es la base del análisis estadístico, ya que en ella se sustenta casi toda la inferencia estadística. (Ricardi, 2011)

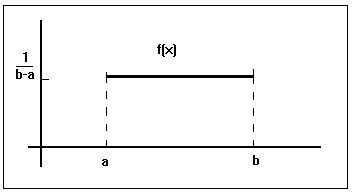
La distribución uniforme, es una parte adentro de la distribución normal, que es una variable aleatoria continua que sus valores se dispersan uniformemente a través del rango de posibilidades. La gráfica de una distribución uniforme presenta una forma rectangular. (TRIOLA, 2005)

2- DISTRIBUCIÓN BINOMIAL

Las distribuciones de probabilidad binomial son importantes porque nos permite enfrentar circunstancias en las que los resultados pertenecen a dos categorías relevantes. (TRIOLA, 2005)

Un experimento binomial presenta las siguientes propiedades:

1. Consiste en un número fijo, n, de pruebas idénticas.
2. Cada prueba resulta en uno de dos resultados: éxito, S, o fracaso, F
3. La probabilidad de éxito en una sola prueba es igual a algún valor p y es el mismo de una prueba a la otra. La probabilidad de fracaso es igual a q=(1-p)
4. Las pruebas son independientes (WACKERLY, SÉPTIMA EDICIÓN)

Vale recordar que en una distribución binomial E y F (éxito y fracaso) denotan las dos categorías posibles de todos los resultados, p y q denotan las probabilidades de E y F respectivamente, donde P(E)= p y P(F)= 1-p = q. (TRIOLA, 2005)

Ejemplo de distribución binomial sacado del libro Mario Triola (TRIOLA, 2005)

                Un profesor planea aplicar un examen sorpresa de opción múltiple, cada una con 5 respuestas posibles (a,b,c,d,e), pero solamente una es correcta. Supongamos que un estudiante sin preparación adecuada hace adivinanzas al azar y queremos calcular la probabilidad de que tenga exactamente tres respuestas correctas en las 4 preguntas.

1. Con cuatro preguntas el examen, tenemos n=4
2. Buscamos la probabilidad de exactamente 3 respuestas correctas, x=3
3. La probabilidad de éxito (respuesta correcta para una pregunta es 0,2), entonces p=0,2
4. La probabilidad de fracaso (respuesta incorrecta), es 0,8, entonces q=0,8

Este ejemplo cumple con las propiedades necesarias para ser una distribución binomial, que vamos utilizar la fórmula:

Entonces la cuenta queda:  = (4). (0,008) . (0,8) = 0,0256

Recordamos que cuando hay 4! Tenemos que hacer 4x3x2x1. (TRIOLA, 2005)

3- DISTRIBUCIÓN DE POISSON

        Es una distribución de probabilidad discreta. Expresa la probabilidad de un número k de eventos ocurriendo en un número fijo si estos eventos ocurren con una frecuencia media conocida y son independientes del tiempo discurrido desde el último evento. (RODRIGUEZ)

        La variable aleatoria x es el número de ocurrencias de suceso en un intervalo. El intervalo puede ser tiempo, distancia, área, volumen o alguna unidad similar. (TRIOLA, 2005)

        La fórmula utilizada es: donde e = 2,71828

        Los requisitos para la distribución de Poisson: (TRIOLA, 2005)

1. La variable aleatoria x es el número de ocurrencias de un suceso durante un intervalo
2. Las ocurrencias deben ser aleatorias
3. Las ocurrencias tienen que ser independientes entre sí
4. Las ocurrencias deben estar uniformemente distribuidas dentro del intervalo que se emplea

La distribución de Poisson tiene los siguientes parámetros:

• La media es µ
• La desviación estándar es σ = raíz cuadrada de µ

4-DISTRIBUCIÓN DE POISSON COMO APROXIMACIÓN DE LA BINOMIAL

                Se utiliza cuando n es grande y p es pequeña, y hay que cumplir dos reglas:

1. N>100
2. Np<10

Si se cumplen dichas condiciones y deseamos utilizar la distribución de Poisson, como aproximación binomial, necesitamos un valor µ, ese valor se calcula utilizando: µ=np.

Bibliografia

Erick Cobo, P. M. (2007). Bioestadística para no estadísticos.

GLANTZ. (SEXTA EDICIÓN). BIOESTADISTICA.

Ricardi, F. Q. (2011). Distribución Normal. MEDWAVE.

RODRIGUEZ, M. R. (s.d.). IMPORTANCIA DE LA DISTRIBUCION BINOMIAL Y DE POISSON.

TAYLOR, B. Y. (s.d.). BIOESTADISTICA.

TRIOLA, M. F. (2005). ESTADISTICA. PEARSON.

WACKERLY, M. S. (SÉPTIMA EDICIÓN). ESTADÍSTICA MATEMÁTICA CON APLICACIONES.